Little Man Computer

The LMC simulator takes the following form:

Main Parts

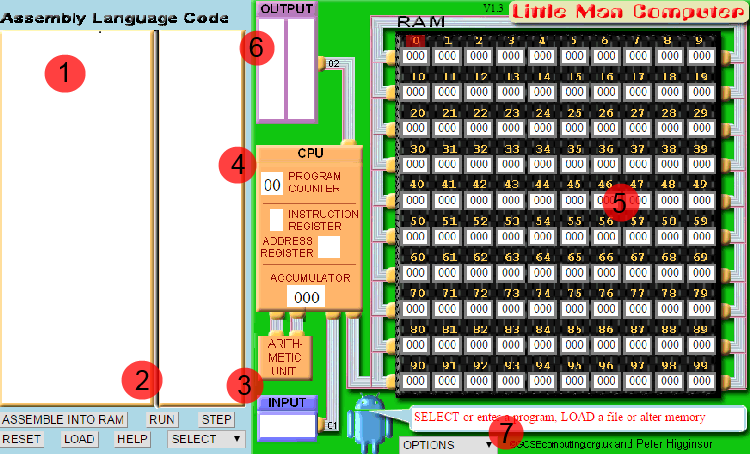
These are main components in the window that are easily recognizable:

1. The window for typing in the code
2. The two buttons - to load the code into memory and then run
3. The window for an input, if any - not necessary
4. An indicator that shows the progress of the code - step by step
5. Memory locations where instructions and data are stored, as specified in von Neumann architecture - 100 cells, from 00 to 99.
6. The window for the output/s during the execution of the code
7. Options for controlling the flow of the execution - slow to fast, etc

The best way to learn the LMC is running set of codes, from the simplest to the more advanced gradually, rather than making an effort to understand the simulator fully at first. This is the approach adopted in this tutorial.

Before that, however, you have to be familiar with the set of instructions: there are not many; just 11 of them. They are as follows:

The basic manipulation of the LMC

First of all, type in the following code in the LMC as shown in the animation in order to see how it works:

The following animation shows how it works:

Please note that not only is the input - 45 - displayed in output window, but also in the memory location 20.

The same can be achieved the following way too - specifying a variable - A in this case - without specifying a particular memory cell.

The following animation illustrates it:

Please note that the value is stored in the fifth memory cell - 045.

Adding Two Numbers

Here is the code for adding two numbers and displaying the sum:

INP 

STA A 

INP 

STA B 

LDA A 

ADD B 

OUT 

HLT

A    DAT

B    DAT

The following animation shows how the two numbers are taken in as two inputs and later answer is given out:

The same can be achieved without providing a user input: the numbers to be added are stored in two variables, instead - A and B.

Subtracting a Number

Here is the code for subtracting the smaller number from the bigger one and then displaying the difference:

The following animation shows how the the smaller number is taken away from the bigger:

The same operation can be carried out exactly like addition; the two numbers can be stored in two different variables, rather than inputting them.

Decision Making

The LMC can be used to model decision making as well. For instance, a number can be taken away from a second number and the output can be sent along a chosen path.

In order to perform operations of this kind, the limited number of loops must be used. They are:
 BRA - branch always.
 BRZ - branch if the outcome is 0.
 BRP - branch if the outcome is positive or zero.

Now, let's use the LMC to determine the bigger of two numbers by using the above loops; the output must be the bigger number regardless of its order of input. This is the code:

The following animation shows how the output always shows the bigger of the two numbers, regardless of the order they are put in:

BRP plays the major role here: it branches out the execution to a sub-route, defined as isPositive., if A-B turns out to be positive. Otherwise, the execution continues along the main route.

Iteration - countdown

The LMC can be used to create a countdown - a form of iteration, with the aid of BRZ and BRA loops. The user provides the programme with an input to generate a countdown. This is the code:

The following animation shows the iteration that leads to a countdown, based on the user input:

Multiplication

The LMC can add or subtract numbers, but it can neither multiply nor divide. The obvious drawback actually makes programming even more interesting: the multiplication, in fact, can be carried out with the aid of addition!

Here is the trick:
2 x 3 = 6
So, 2 + 2 + 2 = 6
3 x 4 = 12
So, 3 + 3 + 3 + 3 = 12

So, with the aid of a loop we keep adding the first number as many as second number of times!

Here is the code for the two inputs:

The following animation shows how two numbers, entered by a user, can be multiplied to produce the product:

Division

As there is no operation to carry out division in the LMC either, this is how subtraction is used to do the division of a number by another:
12 :- 3 = 12 - 3 - 3 - 3- 3 => 4 steps => answer = 4
9 : 3 = 9 - 3 - 3 - 3 => 3 steps => answer = 3

You keep subtracting the divisor - 3 - from the dividend - 12 or 9 - until the answer becomes zero in a loop! In the meantime, a variable must be included in the same loop in such a way that its value goes up by one with every subtraction of the divisor from the divided. Drawing a flow chart will also be helpful. Here is the code:

The dividend and divisor are given as two inputs by the user and the quotient - answer - is given as output:

Squaring a Number

The Little Man Computer can be used to square a number. The procedure is an extension of the process of multiplication.

This is the code for squaring a number:

The output is as follows:

Powers of 2

This code raise the power of 2 to until it produces a three-digit output; it works only for an index that is greater than 0.

1. The first input sholud be number 2.
2. The second input should be the power you want 2 to be raised to, provided that the final answer remains a two-digit number.

The code for the above programme is as follows: